[자료구조] 트리 - 레벨 순회

 

 

트리를 순회하는 방법은 보통 전위 순회, 중위 순회, 후위 순회 방식을 사용합니다.

 

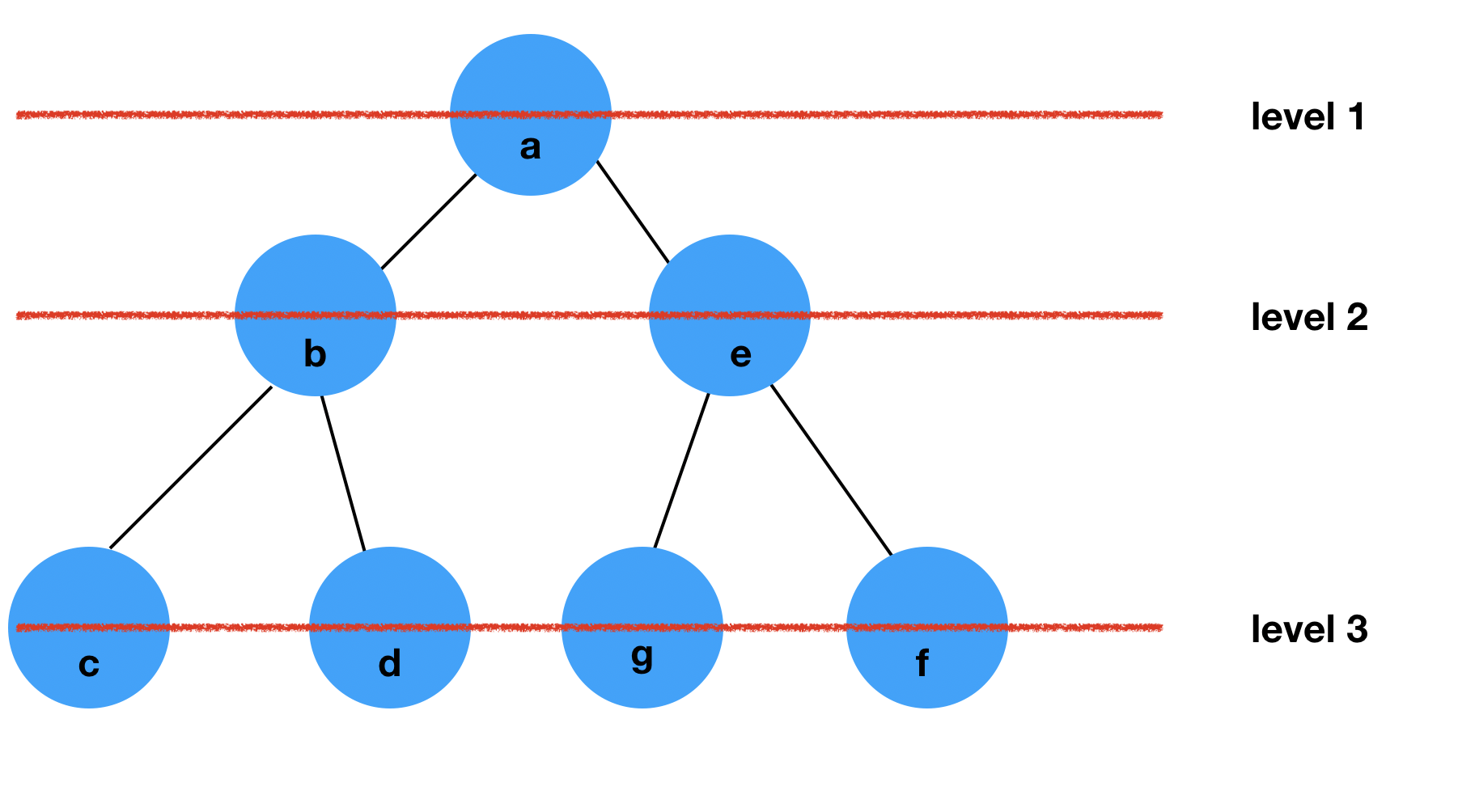
트리 레벨 순회에 대해 파악해봅시다. 우선 트리의 레벨 순회 방법에 대해 알아보기 이전에 트리의 레벨부터 확인해 보아야 합니다.

트리의 레벨은 루트노드를 시작 (level 1)으로 level이 매겨지게 됩니다.

 

 

 

 

 

위 처럼 루트 노드 부터 level 1 이 매겨지고 그 뒤로 루트 노드의 자식들을 따라 level이 결정됩니다.

 

 

 

위의 기준을 통해 레벨 순회는 트리의 각 노드를 레벨 순서대로 방문하게 됩니다. 또한 수업 시간에도 설명하였듯이 왼쪽에서 오른쪽 순으로 노드를 방문하게 됩니다.

 

 

 

즉 노드에 위처럼 문자가 들어있다면, 순회 순서는 

 

a -> b -> e -> c -> d -> g -> f

 

입니다.

 

 

 

지금까지 다른 순회 방법 (전위 순회, 중위 순회, 후위 순회)는 스택 (재귀함수, 순환 호출)을 통해 순획가 이루어졌다면, 이번 레벨 순회의 경우는 큐를 활용하여 순회를 진행하게 됩니다.

 

 

 

간단하게 레벨 순회 알고리즘에 대해 살펴보도록 하겠습니다.

 

1. 큐 생성 및 초기화

2. 큐에 루트 노드 삽입

3. 큐가 empty가 될때까지 반복

    4. Dequeue연산을 통해 노드(N)을 추출 (처음에는 Root node임)

    5. 위에서 추출된 N을 방문

    6. N의 왼쪽 자식이 있다면 그 자식을 큐에 삽입 (Enqueue)

    7. N의 오른쪽 자식이 있다면 그 자식을 큐에 삽입 (Enqueue)

 

 

 

 

위와 같은 방식으로 레벨 순회를 진행하게 됩니다. 이렇게만 확인하면 제대로 확인하기 어렵기 때문에 하나씩 확인해보면서 체크해보도록 하겠습니다.

 

 

 

 

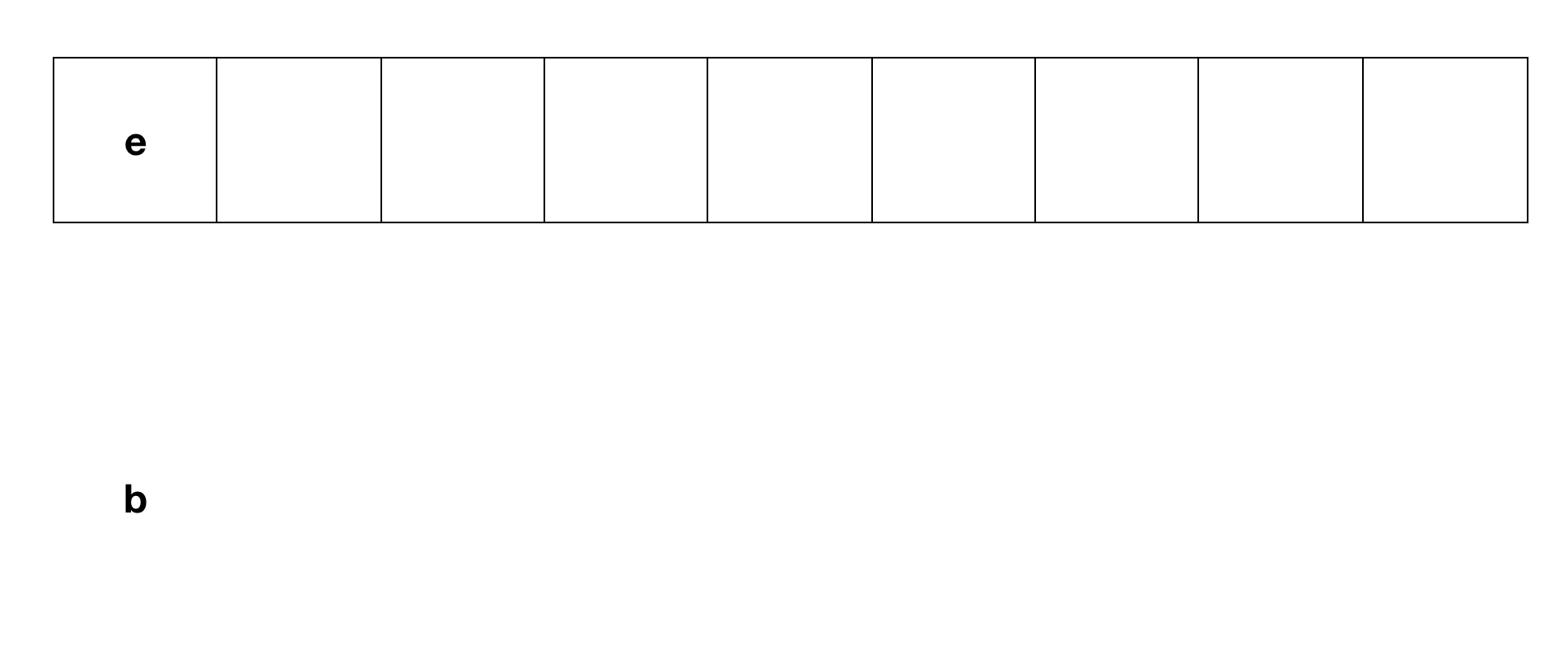
• 큐를 생성 및 초기화를 진행한다.
• 큐에 루트노드를 삽입한다. (Enqueue) ( a 삽입)

• ------ 반복문 시작(1) -------

 

• 큐에서 Dequeue를 진행한다.

• 추출된 노드를 방문한다. (루트노드인 a)
• 방문한 노드의 왼쪽 자식 노드가 존재한다면 (NULL 이 아니라면) Enqueue를 진행한다.
• 방문한 노드의 오른쪽 자식 노드가 존재한다면 (NULL 이 아니라면) Enqueue를 진행한다.

• ------ 반복문 종료(1) -------

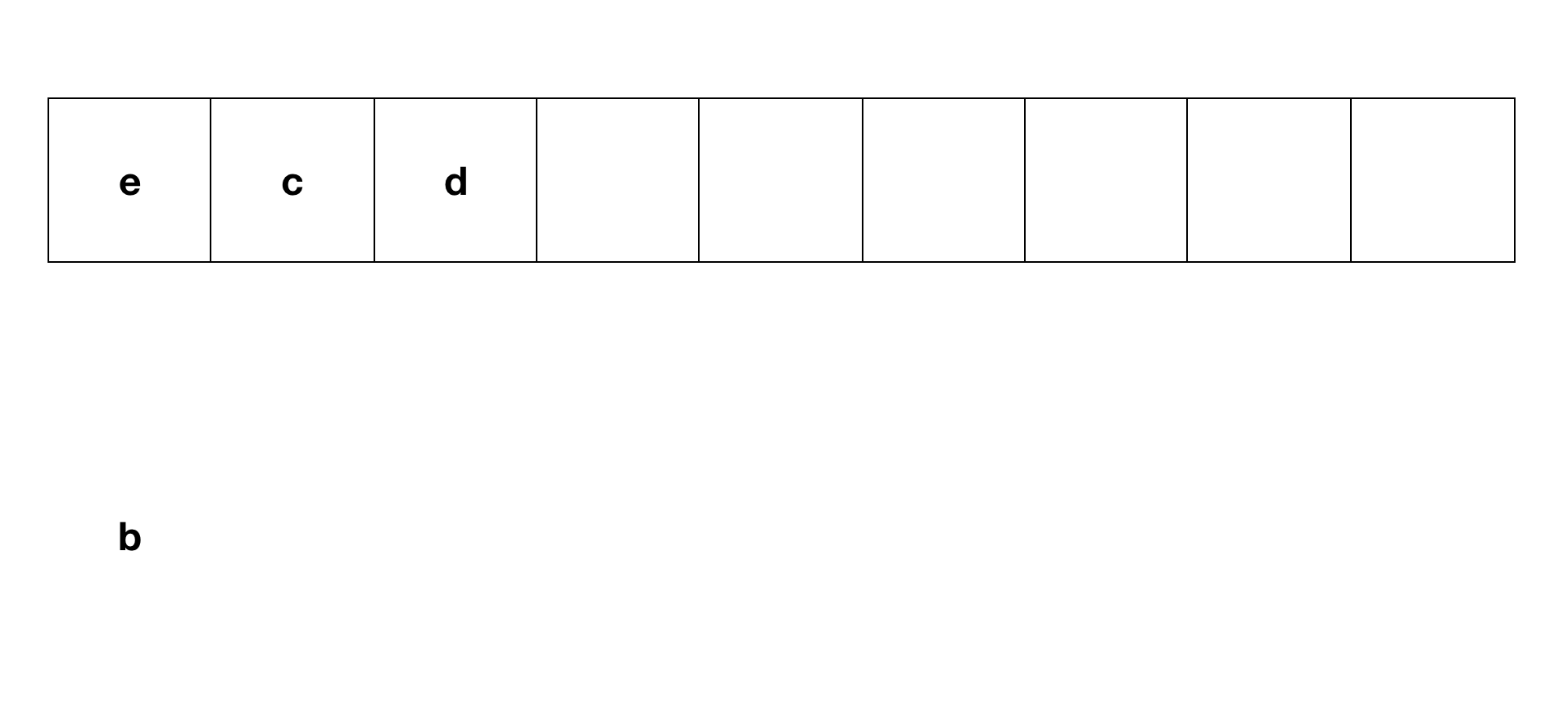
• ------ 반복문 시작(2) -------

• 큐에서 Dequeue를 진행한다.

• 추출된 노드를 방문한다. (노드인 b)
• 방문한 노드의 왼쪽 자식 노드가 존재한다면 (NULL 이 아니라면) Enqueue를 진행한다.
• 방문한 노드의 오른쪽 자식 노드가 존재한다면 (NULL 이 아니라면) Enqueue를 진행한다.

 

 

 

위와 같은 방식으로 레벨 순회가 진행됩니다.

 

 

 

그럼 해당 내용을 예제로 풀이해보도록 하겠습니다.

 

#include <stdio.h>
#include <stdlib.h>

// 연결된 큐 형식을 활용해 구현 진행

// 큐에 삽입될 데이터의 형태를 정의한다. (트리 노드를 의미)
// 구조체 명은 TreeNode라 칭한다. 해당 구조체는 element로 치환되어 데이터영역에 들어가게 된다.
typedef struct TreeNode {
	int data;
	struct TreeNode *left, *right;
} TreeNode;

// 지금까지 자료구조 안에 들어갈 데이터는 항상 element로 치환하여 사용하였다,
// 이번 큐에 들어갈 데이터 타입은 트리의 노드 형태기 때문에 위에서 트리 노드 구조체를 제작하고
// element로 치환한다.
typedef TreeNode * element;

// 큐의 노드타입
// 실직적으로 큐의 노드를 의미한다. 
// 큐를 연결된 형태로 구현할 때에는 단순연결리스트를 활용하기 때문에
// QueueNode의 링크부를 하나만 세팅하였다.
typedef struct QueueNode {
	element item;
	struct QueueNode *link;
} QueueNode;

// 연결된 형태의 큐를 제작한다.
// 수업시간에 확인해보았다 싶이 front와 rear를 바라보는 포인터를 담고 있다.
// front에서는 데이터의 추출
// rear에서는 데이터의 삽입이 일어난다.
typedef struct {
	QueueNode *front, *rear;
} QueueType;

// 오류 함수
void error(char *message)
{
	fprintf(stderr, "%s\n", message);
	exit(1);
}
// 초기화 함수
void init(QueueType *q)
{
	q->front = q->rear = 0;
}
// 공백 상태 검출 함수
int is_empty(QueueType *q)
{
	return (q->front == NULL);
}
// 포화 상태 검출 함수
int is_full(QueueType *q)
{
	return 0;
}
// 삽입 함수
void enqueue(QueueType *q, element item)
{
	QueueNode *temp = (QueueNode *)malloc(sizeof(QueueNode));
	if (temp == NULL)
		error("메모리를 할당할 수 없습니다");
	else {
		temp->item = item; 		// 데이터 저장
		temp->link = NULL; 		// 링크 필드를 NULL
		if (is_empty(q)) { 		// 큐가 공백이면
			q->front = temp;
			q->rear = temp;
		}
		else { 		// 큐가 공백이 아니면
			q->rear->link = temp;  // 순서가 중요
			q->rear = temp;
		}
	}
}
// 삭제 함수
element dequeue(QueueType *q)
{
	QueueNode *temp = q->front;
	element item;
	if (is_empty(q))			// 공백상태
		error("큐가 비어 있읍니다");
	else {
		item = temp->item; 		// 데이터를 꺼낸다.
		q->front = q->front->link; // front를 다음노드를 가리키도록 한다.
		if (q->front == NULL) 	// 공백 상태
			q->rear = NULL;
		free(temp); 			// 동적메모리 해제
		return item; 			// 데이터 반환
	}
}
// peek 함수
element peek(QueueType *q)
{
	element item;
	if (is_empty(q))
		error("큐가 비어 있읍니다");
	else {
		item = q->front->item;	// 데이터를 꺼낸다.
		return item; 			// 데이터 반환
	}
}
// 레벨 순회 
void level_order(TreeNode *ptr)
{
	QueueType q;

	init(&q);
	if (!ptr) return;
	enqueue(&q, ptr);
	while (is_empty(&q)) {
		ptr = dequeue(&q);
		printf(" %d ", ptr->data);
		if (ptr->left)
			enqueue(&q, ptr->left);
		if (ptr->right)
			enqueue(&q, ptr->right);
	}
}
TreeNode n1 = { 1,  NULL, NULL };
TreeNode n2 = { 4,  NULL,  NULL };
TreeNode n3 = { '*',  &n1,  &n2 };
TreeNode n4 = { 16, NULL, NULL };
TreeNode n5 = { 25, NULL, NULL };
TreeNode n6 = { '+', &n4,  &n5 };
TreeNode n7 = { '+', &n3,  &n6 };
TreeNode *exp = &n7;

int main(void)
{
	level_order(exp);
}

 

 

 

위의 코드가 아래의 트리 형태를 레벨 순회로 진행한 것입니다.

 

 

 

레벨 순회에 대한 진행 방식은 위에서 설명하였기 때문에 코드에서는 설명을 진행하지 않았습니다. 직접 공책에 큐와 트리를 그려 어떻게 노드를 순회하는지 확인해보시기 바랍니다.

 

추가적으로 이번에 연결된 큐를 사용할때 큐의 노드에 삽입될 데이터가 트리의 노드기 때문에 element부분이 좀 어려우실 것 같아, 주석을 달아 설명을 진행하였습니다.

 

 

 

만약 위 형태가 이해되지 않는다면, 배열로 구현한 큐 -> 연결리스트로 구현한 큐 -> 레벨순회에서 사용된 큐 순서대로 살펴보시면 이해가 쉽게 되실 겁니다.

 

 

 

이로써 자료구조 트리의 레벨순회를 마치도록 하겠습니다.

 

 

감사합니다.